Fano variety
In algebraic geometry, a Fano variety, introduced by (Fano 1934, 1942), is a non-singular complete variety whose anticanonical bundle is ample.
Fano varieties are quite rare, compared to other families, like Calabi–Yau manifolds and general type surfaces.
Contents |
The example of projective hypersurfaces
The fundamental example of Fano varieties are the projective spaces: the anticanonical line bundle of 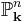 is
is 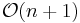 , which is very ample (its curvature is n+1 times the Fubini–Study symplectic form).
, which is very ample (its curvature is n+1 times the Fubini–Study symplectic form).
Let D be a smooth Weil divisor in 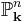 , from the adjunction formula, we infer
, from the adjunction formula, we infer 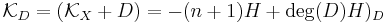 , where H is the class of the hyperplane. The hypersurface D is therefore Fano if and only if
, where H is the class of the hyperplane. The hypersurface D is therefore Fano if and only if 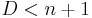 .
.
Some properties
The existence of an ample line bundle on X is equivalent to X being a projective variety, so this is the case for Fano varieties. The Kodaira vanishing theorem implies that the higher cohomology groups 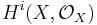 of the structure sheaf vanish for
of the structure sheaf vanish for 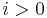 . In particular, the first Chern class induces an isomorphism
. In particular, the first Chern class induces an isomorphism 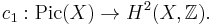
A Fano variety is simply connected and is uniruled, in particular it has Kodaira dimension −∞.
Classification in small dimensions
Fano varieties in dimensions 1 are isomorphic to the projective line.
In dimension 2 they are del Pezzo surfaces and are isomorphic to either 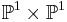 or to the projective plane blown up in at most 8 general points, and in particular are again all rational.
or to the projective plane blown up in at most 8 general points, and in particular are again all rational.
In dimension 3 there are non-rational examples. Iskovskih () classified the Fano 3-folds with second Betti number 1 into 17 classes, and Mori & Mukai (1981) classified the ones with second Betti number at least 2, finding 88 deformation classes.
References
- Fano, G. (1934), "Sulle varietà algebriche a tre dimensioni aventi tutti i generi nulu", Proc. Internat. Congress Mathematicians (Bologna) , 4 , Zanichelli, pp. 115–119
- Fano, Gino (1942), "Su alcune varietà algebriche a tre dimensioni razionali, e aventi curve-sezioni canoniche", Commentarii Mathematici Helvetici 14: 202–211, doi:10.1007/BF02565618, ISSN 0010-2571, MR0006445, http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=209966
- Iskovskih, V. A. (1977), "Fano threefolds. I", Math. USSR-Izv. 11 (3): 485–527, doi:10.1070/IM1977v011n03ABEH001733, ISSN 0373-2436, MR463151
- Iskovskih, V. A. (1978), "Fano 3-folds II", Math Ussr Izv 12 (3): 469–506, doi:10.1070/IM1978v012n03ABEH001994Fano+3-folds+II, MR0463151
- Iskovskih, V. A. (1979), "Anticanonical models of three-dimensional algebraic varieties", Current problems in mathematics, Vol. 12 (Russian), VINITI, Moscow, pp. 59–157, MR537685
- Kulikov, Vik.S. (2001), "Fano variety", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=F/f038220
- Mori, Shigefumi; Mukai, Shigeru (1981), "Classification of Fano 3-folds with B2≥2", Manuscripta Mathematica 36 (2): 147–162, doi:10.1007/BF01170131, ISSN 0025-2611, MR641971Mori, Shigefumi; Mukai, Shigeru (2003), "Erratum: "Classification of Fano 3-folds with B2≥2"", Manuscripta Mathematica 110 (3): 407, doi:10.1007/s00229-002-0336-2, ISSN 0025-2611, MR1969009